Como se ha dicho en la presentación, en esta serie de artículos, en el enunciado, se tratará sobre los principios de la electrónica digital, procurando evitar la parte más compleja siempre que sea posible (como son desarrollo de formulas y principios teóricos, que utilizaremos sólo cuando sean imprescindibles), de manera que le resulte más sencillo de entender a aquel aficionado.
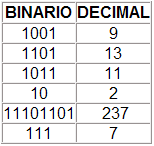
Los que tengan alguna experiencia y quieran avanzar, pueden pasar directamente a la lección 4.
En esta primera lección, veremos:
Sistemas numéricos.
Sistema binario.
Sistemas de numeración binario.
Escritura binaria.
Paso del sistema binario a decimal.
Paso del sistema decimal a binario.
Aritmética binaria.
Complemento de un número.
Códigos del sistema binario.
Código de Gray.
Código hexadecimal.
Álgebra de Boole.
Suma lógica.
Producto lógico.
SISTEMAS NUMÉRICOS.
Desde luego que todos estaremos de acuerdo si decimos que la primera ‘operación’ aritmética que realizó el hombre fue la de contar. La necesidad de contar, le llevó a idear un sistema abstracto, con tantos objetos como dedos tenía en las manos, representándolos con un signo diferente para cada uno, que luego llamaría cifras.
Todos conocemos estos signos abstractos, en la actualidad se utilizan los llamados arábicos, por que son los mas comunes, extendidos y conocidos universalmente.
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Estos signos son los pertenecientes al sistema decimal o de base 10. Debido a la rutina diaria con que utilizamos dicha numeración, hace que algunos no tengamos conciencia de los números que utilizamos, dando por obvio que se componen de unidades, decenas, centenas, etc. De esta forma, cuando alguien habla o escribe un número como por ejemplo 148, nadie repara en que esta cifra esta compuesta por ocho unidades, cuatros decenas y una centena, que puesto en forma exponencial, esto quiere decir, que las unidades se multiplican por 10º, las decenas por 10¹, las centenas a 10², los millares por 10³, etc. Así, la cifra anterior en forma exponencial se representa como sigue:
148 = 1 · 10² + 4 · 10¹ + 8 · 10º
Este sistema decimal, cuya base esta ligada a los diez dedos de las manos, no quiere decir que otro sistema de numeración carezca de importancia. Según esto, un sistema de numeración de hasta 5 signos, tendrá como base B = 5, cuyos dígitos pueden ser 0, 1, 2, 3, 4. Según las necesidades, se puede optar por diferentes códigos como el Binario, Octal, Hexadecimal.
De forma similar para un sistema de numeración hasta dos o sistema de numeración binario, tendrá como base B = 2 el cual sólo tendrá dos dígitos como por ejemplo:
0, 1
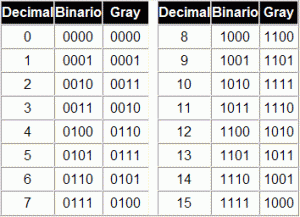
Veamos las equivalencias entre los más utilizados como son el decimal y el binario puro.
| Decimal | Binario | |||
| 0 | = | 0000 | ||
| 1 | = | 0001 | ||
| 2 | = | 0010 | ||
| 3 | = | 0011 | ||
| 4 | = | 0100 | ||
| 5 | = | 0101 | ||
| 6 | = | 0110 | ||
| 7 | = | 0111 | ||
| 8 | = | 1000 | ||
| 9 | = | 1001 | ||
| 10 | = | 1010 | ||
| 11 | = | 1011 | ||
| 12 | = | 1100 | ||
| 13 | = | 1101 | ||
| 14 | = | 1110 | ||
| 15 | = | 1111 |
SISTEMA BINARIO.
Como se ha descrito, el sistema binario utiliza exclusivamente dos números el 0 y el 1, para expresar cualquier magnitud, ahí radica la importancia del sistema binario y la sencillez de sus reglas aritméticas, que hacen del mismo, el sistema ideal para su uso en computadores y otros dispositivos digitales.
Así pies, ya vimos cómo en el sistema decimal se representaba una magnitud, de modo similar se representa en el sistema binario, sólo que en este caso utilizamos dos únicos símbolos el 0 y el 1. Por ejemplo, el número 27 en decimal se representa en binario como 11011. Veamos cómo se representa esto:
11011= 1·24+1·2³+0·2²+1·2¹+1·2°=1·16+1·8+0·4+1·2+1·1=16+8+0+2+1=27
SISTEMA DE NUMERACIÓN BINARIO.
Podemos considerar al sistema de numeración binario como el más extendido después del sistema de numeración decimal. Dicho sistema de numeración binario, nace de la teoría desarrollada por el mencionado matemático inglés George Boole, como ya se ha comentado. Recordemos los estados típicos a los que se puede atribuir la base de numeración binaria:
- Una luz esta encendida (1) o esta apagada (0).
- Un conductor eléctrico con respecto a otro, si tiene tensión está a (1), o (0) si no tiene.
- Un diodo led, si está a (1) luce, se está (0) si no luce.
- Un transistor NPN tiene un estado alto (1) en su colector, si no conduce y si conduce, un estado bajo (0).
- Un relé electromagnético con la bobina excitada, cierra un circuito (1) o abre un circuito (0) si no está excitada.
Todos lo ejemplos mencionados, implican en su concepción un hecho en común, que son ‘biestables’ o sea que, tienen dos únicos estados posibles:
ESCRITURA BINARIA.
Ya que el sistema de numeración binario dispone de dos dígitos (0 y 1). Es lógico pensar que un número binario estará compuesto por una sucesión de estos signos o dígitos y, por consiguiente en una numeración general no podrán tomar otro valor que no sea 0 o 1.
Los anteriores, son números pertenecientes al sistema de numeración binario y su equivalente en sistema decimal.
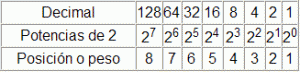
Sería conveniente tener a mano o no olvidar, la siguiente tabla de las potencias de 2, con las que identificar el peso o valor de los dígitos en la posición (o bit) que ocupan para la conversión de un número binario a decimal y viceversa. Esta tabla tendrá mayor relevancia, cuando se estudien los microprocesadores o microcontroladores.
PASO DEL SISTEMA BINARIO A DECIMAL.
Es frecuente utilizar los sistemas binario y decimal y a menudo nos vemos con la necesidad de convertir una cifra de binario a decimal. Bien, en el sistema binario la base es B=2, la expresión general de este sistema de numeración será:
N=Dn · 2n +…+ d3 · 23d2 · 22 + d1 · 21 + d0 · 20
En esta expresión se puede ver que el sistema binario se basa en las potencias de dos. Obsérvese que, un desplazamiento a la derecha equivale a dividir por dos y un desplazamiento a la izquierda en cambio representa multiplicar por dos.
Veamos un ejemplo:
1101 = 1·2³ + 1·2² + 0·2¹ + 1·2º = 1·8 + 1· 4 + 0 · 2 + 1·1 = 8+4+1 = 13 (en decimal10)
Otro ejemplo:
1100111 = 1·26 +1·25+0·24+0·23+1·22+1·21 +1·20= 64+32+0+0+4+2+1=10310
PASO DEL SISTEMA DECIMAL AL BINARIO.
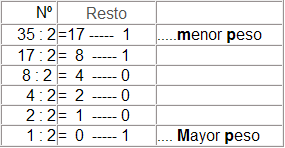
Para efectuar el paso de un número decimal a su equivalente en binario, se puede utilizar el método de las sucesivas divisiones por dos del número decimal dado, los restos de las divisiones se anotan de abajo a arriba y serán los dígitos binarios que representen dicho número. Un ejemplo nos demostrará lo dicho, sea el número decimal 35.
Mp mp
Lo que nos da 35 en decimal = 100011
Otro ejemplo, sea el número 75:
|
1 2 3 4 5 6 7 |
75 : 2 = 37 ----- 1 mp 37 : 2 = 18 ----- 1 18 : 2 = 9 ----- 0 9 : 2 = 4 ----- 1 4 : 2 = 2 ----- 0 2 : 2 = 1 ----- 0 1 : 2 = 0 ----- 1 Mp |
Lo que nos da 75 en decimal = 1001011 en binario.
Es muy conveniente practicar estos métodos de conversión para adquirir cierta soltura al presentarse la ocasión en la realidad.
ARITMÉTICA BINARIA.
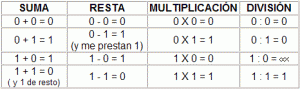
Las reglas de la aritmética del sistema binario son similares a las del sistema decimal, se simplifican mucho al estar compuestas por sólo dos números 0 y 1. A continuación resumimos las cuatro operaciones básicas.
Posteriormente se mostrarán los circuitos que representa estas operaciones. Veamos unos ejemplos de operaciones aritméticas en código binario:
Sumar:
Restar:
Multiplicar:
Dividir:
Estos son, sólo unos ejemplos.
COMPLEMENTO DE UN NÚMERO.
Se le llama complemento de un número, a la diferencia entre la base del sistema y dicho número. La particularidad que presenta es que, la suma del número y su complemento nos dará la base.
Ejemplos:
|
1 2 3 4 |
El complemento de 4 en base 10 es 6 " " 7 " " 10 " 3 " " 3 " " 8 " 5 " " 1 " " 2 " 1 |
Una de las razones para utilizar los complementos es que, pueden realizarse operaciones de resta mediante sumas. El complemento a 1 de un número se obtiene cumplimentando el valor de los bits del número, o sea, cambiando el valor 1 del bit por 0 y el valor 0 del bit por 1. Veamos un ejemplo:
Número: 1 0 1101001
Su complemento a 1: 0 1 0010110
También podemos hallar el complemento a 1, si restamos de 1 todos los bits del número, un ejemplo nos aclarará lo dicho:
|
1 2 3 4 |
111111 001101 ...... número a complementar ---------- 110010 ...... complemento a 1 |
El ‘complemento a 2‘ es el más utilizado por su base. Un método sencillo de hallar el complemento a 2 es, obtener el complemento a 1 y luego sumarle 1 al resultado. Ejemplo:
|
1 2 3 4 5 |
0001101 ......<= número A a complementar 1110010 ........ complemento a 1 +1 ........ se suma 1 ---------- 1110011 ........ complemento a 2 del número A |
Esta es, otra forma de obtener el complemento a 2 de un número. Sea el número binario B (10010), consiste en restar el número (B), al número 1 seguido por tantos ceros como bits tenga el número B, veamos un ejemplo:
|
1 2 3 4 |
100000 .... número 1 seguido de 5 (ceros) bits que tiene el número B -10010 .... número B a complementar --------- 001110 .... complemento a 2 de B |
Bien, hemos visto aunque de pasada, cómo hallar el complemento de un número y el complemento a 2, ahora daremos un paso más dentro de los códigos.
CÓDIGOS DEL SISTEMA BINARIO.
Los códigos en general, se pueden expresar de dos modos: 1) como ‘código ponderado’, cuando hace referencia a la posición que ocupa el bit de un número llamado también peso (BCD, HEXADECIMAL). Y 2) ‘código no ponderado’, de este tipo uno muy utilizado es el exceso a 3, código de Gray y otro el de paridad entre otros.
Sistema BCD (Binario Decimal Codificado).
Se llama sistema BCD a una forma particular de anotar el sistema binario, para contar y representar números en decimal. Cada dígito decimal se expresa por 4 bits, véase la tabla siguiente:

Tabla de los números decimales codificados en BCD y binario natural.
Fig. 6
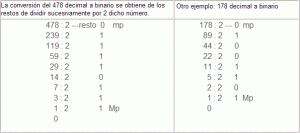
De forma que utilizando esta tabla el número decimal 478, se representará en BDC de la siguiente forma:
|
1 2 |
Decimal: 4 7 8 BDC: 0100 0111 1000 |
Esta es la forma de representación habitual utilizada en las computadoras, por ese motivo los códigos siempre son múltiplos de 4.
Lo que se expresa por: 111011110 y 10110010 respectivamente, como se aprecia, no es lo mismo binario natural que codificado a BCD, como vimos en el caso anterior.
Ciertamente hay unos tipo de codificación muy generalizados para las diferentes necesidades por parte de los técnicos, ahora veremos superficialmente el de exceso de 3 y hexadecimal que son los más usados.
Código de Gray.
En el código de Exceso a 3 respecto al BCD, sus dígitos no dependen de su peso o magnitud concreta, con la diferencia respecto de él por que se ha sumado 3 a cada dígito. Es decir, al valor de un número en BCD, se le suma 3 a cada dígito para codificar y se le resta 3 para decodificar y obtendremos el valor en Exceso a 3 o XS3.
En cuanto al código Gray, es un código sin ponderar conocido como código binario reflejado o cíclico y a cauda de que minimiza los errores, llamado también como código de errores mínimo en ciertas operaciones.
Este código, se utiliza cuando hay rotaciones de ejes, movimientos radiales o desplazamientos, convirtiendo estos movimientos en un valor binario equivalente (proceso y control de máquinas), para que el computador pueda procesar dichos datos y pueda calcular, procesar dicha información.
Las líneas de transmisión de datos, los convertidores de analógico a digital, entre otros, introducen errores cuando cambian grupos de bits en la conversión. Por ejemplo, al pasar en binario de 0111 a 1000 (7 a 8), de 1111 a 10000 (15 a 16) etc. En la tabla de debajo, se aprecia en el código de Gray, que sólo cambia un bit al pasar de un número al siguiente superior. El lector puede aumentar fácilmente este código, siguiendo la pausa que lo caracteriza, sumando el número binario con sigo mismo sin acarreo, se trata de sumar sin acarreo.
Otra forma, añadiendo en cada columna desde la derecha un 0 o un 1, según corresponda, observar en la tabla la cadencia, por ejemplo; 1,2 – 11 : 3,4 – 00 : 5,6 – 11, etc.
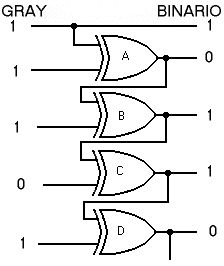
Se pueden utilizar circuitos EOR semi-sumadores para convertir código Gray a binario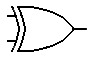 . Recordemos que una puerta EOR (XOR) de dos entradas, su símbolo se muestra en la figura de la derecha, por si misma nos proporciona un sumador sin acarreo o semi-sumador.
. Recordemos que una puerta EOR (XOR) de dos entradas, su símbolo se muestra en la figura de la derecha, por si misma nos proporciona un sumador sin acarreo o semi-sumador.
Ver en la imagen siguiente un ejemplo de conversión del número 11101 de código Gray a su equivalente en código binario. este número se aplica a las entradas de la izquierda y su salida (derecha) presenta el número 10110 en binario, el 16h en hexadecimal y el 22 en decimal.
Sin embargo, no se debe confundir el código Gray con los códigos detectores de error. Un código muy difundido capaz de detectar errores de cálculo en sistemas de comunicación es el llamado comprobación de paridad de bit. Es un código que indica si el número total de bits 1 es par o impar y se utiliza para detectar errores de la forma más sencilla.
Se llama ‘paridad’ a la particularidad de ser ‘igual’ y por esto la comparación de paridad utilizando un código que genere un número de dígitos par o impar añadiendo un dígito al grupo. Al dígito añadido se le llama dígito de paridad y puede ser un 1 o un 0. En consecuencia un número binario de 4 bits, al aplicarle el bit de paridad, se representa por un grupo de 5bits. Debido a que el bit o dígito de paridad circula siempre unido al número binario, se puede detectar un error inmediatamente ya que cambia la paridad del número.
CÓDIGO HEXADECIMAL.
Es un sistema de base 16 y se representa por los mismos dígitos 0 al 9 además de las 6 primeras letras mayúsculas del abecedario, A, B, .. F. Actualmente es el sistema preferido para los procesadores de datos, además, al tener 16 números y ser 16=24, todos los números del sistema hexadecimal se suelen expresar por grupos de 4 bits o dígitos, lo que simplifica la escritura de números binarios, facilitando la conversión entre hexadecimal y binario, otra ventaja. El modo de expresar un número hexadecimal suele hacerse añadiendo una ‘h’ a continuación de los dígitos que lo componen.
Por ejemplo, para pasar el número hexadecimal 7C8h, a binario, bastará con pasar cada dígito a binario por separado, es decir, 7=0111, C=1100 y 8=1000, lo que se representa por:
0111 1100 1000 = 7C8h
Por lo tanto, para convertir un número binario a hexadecimal, empezaremos por agrupar los bits de 4 en 4, para ello añadiremos los ceros que sean necesarios. Es decir, dado el número binario anterior 11111001000, para pasarlo a hexadecimal, primero debido a que tiene 11 dígitos, completaremos con un cero los 12 bits, para formar tres grupos de 4 y quedará como sigue:
0111 1100 1000
Ahora, para ver mejor lo que se ha dicho cambiaremos la disposición y su valor en hexadecimal.
- 0111 = 716
- 1110 = C16
- 1000 = 816
Es decir que: 7C816 = 011111101000
Para convertir un número binario a hexadecimal, agruparemos los bits de 4 en 4 añadiendo para ello, los ceros necesarios, convirtamos el número binario 110 1010 0011, como tiene 11 dígitos añadimos un cero no significativo a la izquierda, para cumplir la regla, sigamos:
- 0110 1010 0011
- 0110 = 616
- 1010 = A16
- 0011 = 316
O sea, 6A316 o en la forma más común 6A3h.
La conversión más utilizada es la de convertir un número hexadecimal a decimal y viceversa, por ser la más cercana al lenguaje máquina una y al lenguaje humano la otra. Veamos cómo convertir a decimal el número 37Fh:
37F16 = 3·16²+7·16¹+15·16° = 768+112+15 = 89510
Ahora, convirtamos el número 1.35710 a hexadecimal, lo iremos dividiendo por 16 sucesivamente hasta que no se pueda continuar, formando el número en hexadecimal el cociente seguido de los restos desde el último al primero, veamos:
|
1 2 3 4 |
1357 : 16 = 84 13 84 : 16 = <strong>5</strong> | <strong>4</strong> <strong>D</strong> |
Esto es: 135710 = 54D16
También podemos convertir el 135710, primero a binario: 10101001101 y luego separamos de derecha a izquierda en grupos de 4, así obtendremos:
|
1 2 3 4 |
0101 = <strong>5</strong><sub>16</sub> 0100 = <strong>4</strong><sub>16</sub> 1101 = 13<sub>10</sub> = <strong>D</strong><sub>16 </sub> |
Como se puede observar obtenemos el mismo resultado.
ÁLGEBRA DE BOOLE.
El álgebra de Boole, establece que todos los elementos tienen dos estados únicos y basándose en esta teoría, establece unos postulados y operaciones para resolver las ecuaciones que representan los automatismos y/o procesos establecidos, obteniendo unos resultados que se deben traducir y ejecutar por sistemas electrónicos, mecánicos, neumáticos o hidráulicos.
Desde el punto de vista del álgebra de Boole, el estado de cualquier elemento es cierto o falso, o sea, en el caso de un interruptor estará cerrado o abierto, una lámpara estará encendida o apagada, un relé estará activo o en reposo. Debido al hecho de que sólo se consideren dos estados, es lo que ha llevado a llamarla álgebra binaria o también álgebra lógica por comportarse de modo intuitivo y lógico. Esto permite representar por símbolos, objetos de un circuito lógico con equivalencia al circuito real representado.
La suma lógica (OR).
De dos variables, se expresará en forma eléctrica como dos interruptores conectados en paralelo, obteniendo cuatro estados posibles, de los cuales sólo uno corresponde al estado de circuito abierto, ya que únicamente cuando los dos interruptores estén abiertos también lo estará el circuito.
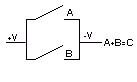 Fig. 11
Fig. 11
El producto lógico (AND).
De dos variables, en forma eléctrica se expresará como dos interruptores en serie, de cuyos cuatro estados posibles, sólo en el caso de estar ambos cerrados, también lo estará el circuito eléctrico al que pertenecen.
Las operaciones NOR y NAND representan una inversión de las anteriores, para hacernos una idea, eléctricamente se puede entender como pulsadores normalmente cerrados, en lugar de interruptores normalmente abiertos.
Si alguna cuestión no ha quedado clara, deberías indicármelo como siempre.




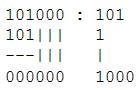
Hola Mónica.
Gracias por tus palabras.
Gracias, está explicado muy simple.