En la lección anterior de esta serie, se presentaron los principios básicos de la lógica de Boole, en los que se basa la electrónica digital, procure tener claros estos conceptos antes de continuar, ya dijimos que procuraremos evitar en lo posible el desarrollo de formulas y principios teóricos, aunque hay un mínimo que resulta inevitable, mediante los cuales le resultará más sencillo de entender.
En esta lección, veremos:
Un poco mas de teoría.
Puertas y Símbolos lógicos.
Leyes teoremas y axiomas.
UN POCO MÁS DE TEORÍA.
Los que tengan alguna experiencia y quieran avanzar, pueden pasar a la lección 4.
Si no es el caso siga con nosotros y verá que en nuestros días, todos los computadores digitales, centros de control electrónico, centros de transmisión de datos u otros elementos de tratamiento de señales como la Internet, las cámaras, la TV, sonido, DVD, WAP, etc. se sirven de circuitos de conmutación con mayor o menor complejidad por medio de los cuales se logran efectuar tareas de forma económica y eficiente. De hecho, estos centros de control, prácticamente disponen de los mismos equipos, en la mayoría de los casos, son los programas los que producen resultados diferentes, esto es lo que los convierte en distintos. La ventaja inherente a todos ellos es la flexibilidad que les confiere la programación.
El principio de la lógica, basada en dos únicos estados posibles, a los que se tiende en cada instante, se pueden considerar como el nivel alto o H, y el opuesto nivel bajo o L, también se llaman ‘estado alto’ y ‘estado bajo’ o ‘cierto’ y ‘falso’ y comúnmente en las máquinas y programas que las controlan, en realidad se comunican en lenguaje máquina, es decir que, se representan por 1 y 0 respectivamente, este es el motivo por el que se denomina lenguaje máquina, ya que está más cercano a las máquinas que a los humanos. Nosotros, utilizamos el lenguaje con fonemas, formado por silabas y sonidos que, las máquinas no pueden entender (por ahora).
En término literal de pensamiento, en electrónica que es el punto de vista que vamos a considerar en este manual, utilizaremos indistintamente estos términos, para que se familiarice el lector.
Debido a que la computación se rige por numerosas condiciones lógicas, el diseño y montaje de estos sistemas exige un estudio ordenado que incluye ciertas reglas lógicas. La mejor herramienta para acelerar la formación de sistemas de conmutación lógica eficiente y para analizar sus características de funcionamiento es utilizar la mencionada álgebra de Boole, la cual como ya se ha indicado, trata del estudio de variables que se limitan a dos valores únicos: ‘uno’ y ‘cero’, estos valores corresponden a los estados ‘abierto’ y ‘cerrado’ o ‘cierto’ y ‘falso’ como estados del circuito eléctrico o electrónico.
Considerando un sólo interruptor de cualquier sistema, resulta un elemento sencillo que tiene un estado abierto AP [apagado] ‘off’ y un estado cerrado EN [encendido] ‘on’, sencillo.
Así, si consideramos uno sólo de los conmutadores de cualquiera de los sistemas citados, estaremos ante un sencillo elemento que sólo dispone de un ‘nivel alto’ o ‘nivel bajo’. Si lo que consideramos es una serie de estos elementos conectados en secciones, unas, en serie y otras en paralelo o mixtas, estaremos ante un sistema de red que continuará siendo sencilla de inspeccionar y no parece capaz de ocasionar grandes problemas en su seguimiento a un técnico.
En realidad, los sistemas de conmutación utilizados en computadoras, no siempre se basan en estructuras sencillas como ‘todo’ o ‘nada’. A menudo, éstas se rigen por órdenes ‘lógicas’ o secuenciales, o sea que, la condición ‘cierto’ o ‘falso’ se dará solamente cuando se cumplan unas determinadas condiciones.
A este hecho, además de la necesidad de que hayan numerosas señales circulando por pistas múltiples (llamadas ‘bus’), hace que el circuito final sea tan complejo que, no se pueda diseñar o aplicar por un simple trazado o por intuición, aun habiendo diseñadores competentes. Al final, el circuito tendrá mas interruptores de los necesarios para realizar sus funciones. Por lo que el sistema será menos fiable y más costoso de mantener, a parte de otras circunstancias.
Este es, el principal motivo de la necesidad de una base teórica mínima, ya que sin ella nos quedaríamos atascados con suma facilidad. Lo más importante es el concepto, siempre nos reiteraremos en esto.
Veamos, el álgebra de Boole, considera a todos los elementos con los que se cuenta, como biestables, elementos con dos únicos estados posibles y complementarios. No existen estados intermedios.
Esto es por lo que el álgebra de Boole (también conocida indistintamente como álgebra binaria o álgebra lógica), es un sistema matemático utilizado en el diseño de circuitos electrónicos digitales, para representar estos objetos del circuito lógico, que se apoya en símbolos que definen su estado lógico.
En otras palabras, se trata de un sistema matemático con el que representar unos grupos de objetos mediante símbolos con los que se definen unas leyes que cumplen sus funciones y sus interrelaciones, expresando unos estados productos de unas ecuaciones que se representan de forma simbólica.
Los mencionados símbolos se utilizan para representar entradas y salidas de los diferentes elementos lógicos con sus estados que cumplen las ecuaciones que definen las diferentes puertas lógicas y otros circuitos más complejos, como ya veremos.
Quizás lo más importante sea, obtener la forma de una ecuación lógica que interprete los procesos, utilizando las operaciones necesarias cuyos resultados sean de aplicación demostrable.
Ya hemos visto anteriormente la representación simbólica de la suma y el producto lógicos para dos elementos que es lo mismo que para tres o más.
PUERTAS Y SÍMBOLOS LÓGICOS.
Ahora, vamos a presentar las puertas y símbolos lógicos básicos que se reconocen internacionalmente y que nos ayudarán a manejar, seguir y comprender las ecuaciones que abordaremos en los próximos ejercicios y lecciones, símbolos de los que nos surtiremos para sentar los conocimientos que se vayan desarrollando.
Las puertas para simplificar se presentarán con el mínimo de entradas, por lo tanto la puerta AND de dos entradas y su tabla de verdad se pueden ver en la figura.
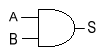
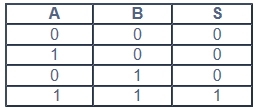
La puerta OR como ya se ha descrito y su tabla de verdad se presentan a continuación.
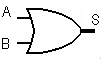
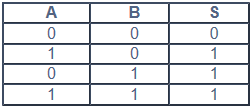
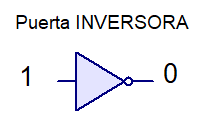
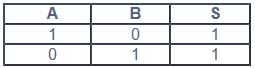
La puerta inversora siempre tiene una única entrada y una única salida y su tabla de verdad se muestra debajo.
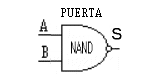
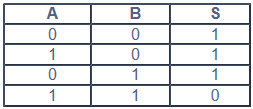
Al aplicar una inversión a una de estas puertas obtenemos las respectivas negadas de las primeras, como la NAND.
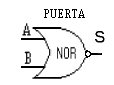
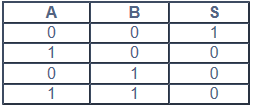
Ahora representación de la puerta y símbolo correspondiente al NOR.
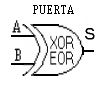
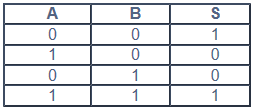
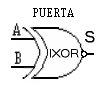
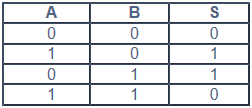
Las puertas EOR o conocidas por EXOR, es una puerta OR Exclusiva, en la que la salida es verdad cuando sus entradas son iguales, independientemente del nivel o estado, es decir los dos de afuera.
También existe la inversa de la EOR, aunque menos usada llamada Inclusive OR o IOR, en esta su salida es verdad cuando sus entradas son distintas entre si, es decir los dos de adentro.
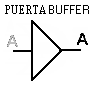
Y el caso del amplificador de señal, que se utiliza para reforzar una señal débil, se le conoce como Buffer.
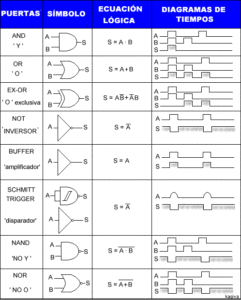
Se presentan dos tablillas que deberían copiarse a impresora, para disponer de ellas y consultarlas.
TABLA DE SÍMBOLOS LÓGICOS BÁSICOS.
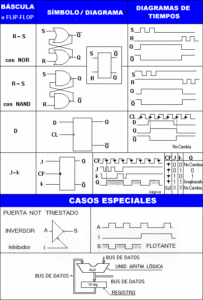
Y ahora, la tabla de lógica sencilla como son las diferentes básculas y sus tipos.
TABLA DE SÍMBOLOS Y LOGIGRAMAS SENCILLOS.
Se recomienda al lector que haga una copia por impresora de las dos tablas precedentes y las tenga a mano para un mejor seguimiento de las lecciones y consulta de uso personal.
Creo que ahora, ya disponemos de una herramienta de ayuda que espero cumpla su cometido. Bien, sigamos, doy por sentado que el lector sabe deducir la tabla de verdad de las distintas puertas y sus respectivas combinaciones a pesar de que en algunas ocasiones nos veremos forzados a presentarlas para una mejor comprensión o por hacer hincapié en lo que se esté tratando.
Veamos algunas cuestiones que puede que no estén muy claras, como por ejemplo, la representación eléctrica del complemento, véase la figura 2-1.
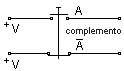
fig. 2-1 Representación eléctrica del complemento de un nivel.
LEYES, TEOREMAS Y AXIOMAS.
Si, de vuelta con la teoría, tratemos de entender, es necesario y nos irán muy bien los párrafos siguientes sobre los axiomas.
El 1er axioma, dice que el producto de ‘1’ por una variable es igual a dicha variable, véase la siguiente representación eléctrica y el símbolo de la ecuación lógica, en la fig. 2-2.
A * 1 = A
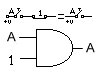
Fig. 2-2
En cambio en el 2º axioma, nos dice que una variable más (OR) el nivel unidad, siempre equivale al nivel unidad, veamos la figura 2-3.
A + 1 = 1
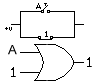
Fig.2-3
El 3er axioma nos dice que el producto de un contacto abierto (nivel 0) por una variable cualquiera, siempre nos presentará un resultado de 0, o dicho de otro modo, un contacto abierto en serie con una variable cualquiera, siempre será un contacto abierto, como se puede ver en la figura 2-4.
0 * A = 0
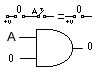Fig. 2-4
El 4º axioma, de forma similar, nos indica que contacto abierto en paralelo (OR) con una variable cualquiera, no tiene ninguna influencia en el resultado, véase la figura 2-5.
0 + A = A
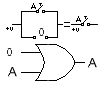
Fig. 2-5
Veamos el 5º axioma, dice que el producto de una variable por su complemento equivale a un circuito abierto o también llamado variable vacía.
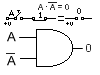
Fig. 2-6
Y por último en el 6º axioma, el cual dice que la suma de una variable y su inverso equivale un estado alto (H) o sea, la unidad (1).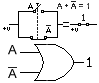
Fig. 2-7
Esperamos que hayan quedado claros los conceptos explicados, forman parte de la base de los futuros conocimientos necesarios, con los que podremos reducir las ecuaciones complejas y con ello las puertas que sean innecesarias.