EQUIVALENCIAS CONTACTOS-PUERTAS.

Los circuitos eléctricos descritos como Y (AND) y O (OR) que vimos en la anterior lección, cuando se representa como dispositivos lógicos en sistemas electrónicos, son denominados como de tipo sólido. El hecho de ser de estado sólido (por su constitución y miniatura), permiten una velocidad de conmutación elevada y casi están exentos de averías, que son tan comunes en elementos mecánicos.

En esta lección veremos:

Conmutadores con diodos
Equivalencias entre contactos y puertas
Resolución de problemas
Primer problema
Segundo problema
Tercer problema
Cuarto problema

LOS DIODOS COMO CONMUTADORES.

Los diodos nos permiten formar circuitos conmutadores con un mínimo de elementos, con los cuales podremos realizar ciertos tipos de puertas lógicas, y adquirir cierta práctica en esta disciplina que al mismo tiempo reforzará la teoría que representan, además de ser muy económicos.

Los circuitos Y (AND), O (OR) y NO (INV), se describen y analizan representando sus características mediante expresiones booleanas, tablas de la verdad, diagramas de Venn y grafos de Karnaugh. Estos circuitos se pueden combinar para efectuar procesos lógicos específicos, la aplicación de las expresiones algebraicas a dichos procesos, nos permiten simplificar los circuitos finales.

En esta parte se tratan ciertos aspectos importantes de los conmutadores lógicos de estado sólido. Las bases que se describen nos servirán como ayuda al estudio del álgebra de Boole y los ejercicios que se describen en adelante.

Ya explicamos con anterioridad los estados alto y bajo según la lógica 1 y lógica 0. De este modo al analizar cualquier circuito eléctrico, podremos ver que está compuesto por cierto número de contactos dispuestos, bien en serie, paralelo o mixtos, cuyo propósito es gobernar un receptor.

EQUIVALENCIAS ENTRE CONTACTOS Y PUERTAS.

-Imaginemos un circuito, compuesto por tres contactos eléctricos, en una disposición mixta, cuyo cometido es activar un relé R-.
La disposición de estos contactos, no se especifica, pero sobre ellos sabemos que cada uno puede optar por el estado de ‘abierto’ o ‘cerrado’. Entre las posibles combinaciones de estos contactos, el enunciado nos dice que hay una disposición que producirá la conducción del circuito de modo que el relé entrará en conducción y el resto de las combinaciones no permitirán la conducción del circuito, por lo que no habrá paso de corriente y no se activará el relé.

En conclusión, cualquier circuito eléctrico puede estar compuesto por cierto número de variables binarias o variables independientes, los cuales dan como resultado una función como variable de salida.

Basándonos en lo expuesto, el álgebra lógica representa las variables de entrada de un circuito por medio de letras, agrupadas convenientemente, de acuerdo a ciertas condiciones preestablecidas, sujetas a reglas operativas, dando lugar a expresiones algebraicas de las variables binarias que podrán ser transformadas y simplificadas, dando una expresión fácil de traducir a un circuito eléctrico o electrónico que cumplirá las condiciones del enunciado.

Para obtener las expresiones algebraicas correspondientes a un circuito dado, en dos principio establecidos.
◾Los contactos en serie, se corresponden en la práctica con la función Y o producto lógico.
◾Los contactos en paralelo, se corresponden en la práctica con la función O o suma lógica.

El primer objetivo es simplificar al máximo las funciones algebraicas para lo que tendremos en cuenta que todos los contactos que mueve un mismo relé, un pulsador o mecanismo, se pueden representar por una misma variable, atendiendo a la diferencia entre un contacto normalmente abierto (NA) representado por una letra, o normalmente cerrado (NC) representado por una letra negada.

El método generalizado a seguir, hasta tener un cierto grado de práctica, consiste en obtener la expresión algebraica de un determinado circuito eléctrico, mediante el recorrido de todos los posibles caminos del circuito desde la entrada a la salida, asociándolos todos ellos en paralelo. Este método, nos permitirá adquirir práctica y acabará por no utilizarlo en la medida en que se acostumbre con las expresiones algebraicas de los circuitos, ya que las obtendrá de forma intuitiva.

Por lo tanto con contactos eléctricos fig. 4-1, se pueden reproducir circuitos, los cuales se pueden simplificar mediante el álgebra de binaria, véase el ejemplo siguiente:

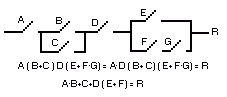
Fig.4-1

A continuación vemos en la fig. 4-2, otra disposición de unos contactos y su función equivalente, para familiarizarse con este tipo de circuitos.

Fig.4-2

Seguidamente en la figura 4-3, se muestran unos ejemplos de sumas y productos lógicos y sus equivalentes con puertas que producen el mismo resultado. Este montaje, tiene la propiedad distributiva que se le atribuye al producto lógico.

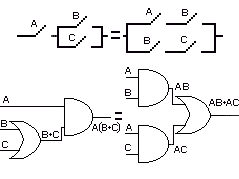
Fig.4-3

Y en la siguiente figura 4-4, se puede apreciar una segunda propiedad distributiva del producto lógico.

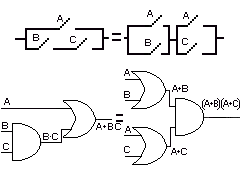
Fig.4-4

También, se puede apreciar estas propiedades mediante la tabla de la verdad, en cada caso. De esta forma, podemos interpretar los contactos de un circuito eléctrico o electrónico a la hora de reducir una función dada o al revés, plantear un circuito eléctrico a partir de una función lógica, como resultado de un enunciado.

Para acercarnos más a lo que tratamos de explicar plantearemos unos problemas reales.

RESOLUCIÓN DE PROBLEMAS.

En esta ocasión, nos proponemos dar solución a problemas concretos sobre exigencias de los circuitos que necesitamos aplicar en el campo de la industria. Por lo tanto, cuando se presente una ocasión de plantear un circuito que solucione una situación, primero deberemos anotar un enunciado en el que se describan todas las necesidades que exija cada situación, con tantos contactos como sean necesarios para cumplir con las exigencias del circuito propuesto.

El segundo paso es crear una tabla de verdad que cumpla todos los supuestos del enunciado. Luego entramos en la elaboración de la ecuación o función que nos proporciona la mencionada tabla de verdad y seguidamente trataremos de reducir por simplificación las ecuaciones y finalmente trazaremos el esquema eléctrico y el lógico que, cumpla la función.

PRIMER PROBLEMA.

Deseamos controlar el estado de una lámpara mediante dos interruptores A y B, partiendo de que si estos están abiertos la lámpara estará apagada pero cada vez que uno de ellos varíe el estado, la lámpara cambie de apagado a encendido y viceversa.

En la primera fase, estableceremos la tabla de verdad, el enunciado nos indica que hay dos variables A y B, la lámpara que es la salida y el estado inicial definido, donde si A= 0 y B=0 la salida L=0.

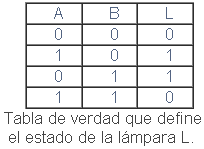
Se aprecia que la lámpara sólo se ilumina en dos casos, según la tabla de verdad.

A=1 y B=0 —– (A·B) …. -esto se lee: A y B negada
A=0 y B=1 —– (A·B) …. -esto se lee: A negada y B
En la segunda fase, obtendremos la función o ecuación lógica. De la anterior fase ha quedado claro lo va a ser la ecuación con sus estados.

L=A·B + A·B

La tercera fase, comprende la simplificación de la ecuación. Sólo que en este caso por su sencillez no existe un elemento que pueda ser factor común para simplificar la ecuación, por lo tanto se pasa a la fase siguiente.

Esta es la fase de la representación eléctrica de la función.

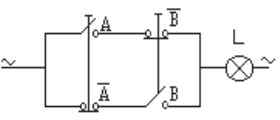
Fig. 4-5 -Representación eléctrica
de la ecuación.

Y fase quinta, el esquema lógico de la función.

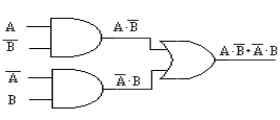Fig. 4-6 -Representación lógica
de la ecuación

En el esquema lógico final se ha obtenido el resultado pedido en el enunciado mediante elementos eléctricos o electrónicos o neumáticos, los cuales realizan las operaciones booleanas que indica la ecuación. Más adelante se simplificará con inversores las funciones de las entradas negadas.

SEGUNDO PROBLEMA.

Queremos controlar dos motores M1 y M2 mediante los contactos de tres interruptores que llamaremos A, B y C. Pero deben cumplirse las condiciones que siguen:
a) Si A está cerrado y B y C no, se activará M1
b) Si C está pulsado y A y B no, se activará M2
c) Si A, B y C están cerrados se activarán M1 y M2

El resto de combinaciones no activarán ninguno de los dos motores.

En la 1ª fase, creamos la tabla de verdad, según este enunciado.

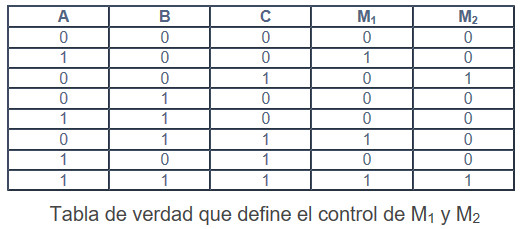
Pasemos a la 2ª fase para obtener la ecuación lógica que en este caso serán dos, que cumpla estas condiciones, del enunciado se deducen las condiciones exigidas o de la misma tabla de verdad.

Para M₁: A está cerrado y B y C abiertos (A·B·C), o A, B y C están cerrados (A·B·C)

  1–  M₁ = A· B· C + A·B·C

Para M₂: si A y B están abiertos y C cerrado (A · B·C), o también si A y B y C cerrados (A·B·C).

  2– M₂ = A· B·C + A·B·C

En la 3ª fase, simplificamos ambas ecuaciones que a simple vista en la función 1 se puede sacar factor común A y lo mismo ocurre en la segunda 2 cuyo factor común es C. Así pues:

M₁ = A· B· C + A·B·C  =  A  (B·C + B·C)
M₂ = A ·B ·C + A·B·C  =  C  (A· B + A·B)

Pasemos a la 4ª fase para representar dichas ecuaciones, veamos:

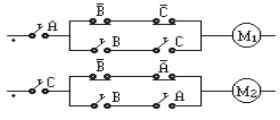
Fig. 4-7 -Representación de las dos
ecuaciones para controlar M1 y M2

Y por último en la 5ª fase, el esquema lógico que representa las funciones de M1 y M2. Mediante inversores se simplifican las entradas.

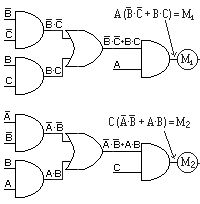
Fig. 4-8 -Esquema lógico de las
funciones M1 y M2

Y esta sería la función definitiva.

 
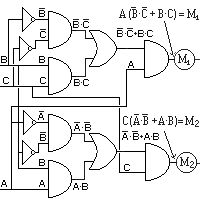
Fig.4-9

TERCER PROBLEMA.

Determinar el circuito eléctrico y lógico que cumple esta propuesta. Mediante tres pulsadores A, B y C queremos controlar la puesta en marcha de dos motores M1 y M2, según el siguiente criterio:

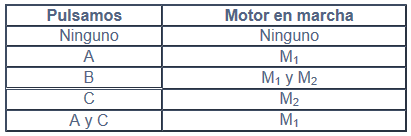
Cuando la propuesta considera dos receptores (al igual que en el problema anterior), se deben considerar el uso de dos circuitos y por lo tanto dos funciones.

Primera fase, la tabla de verdad.

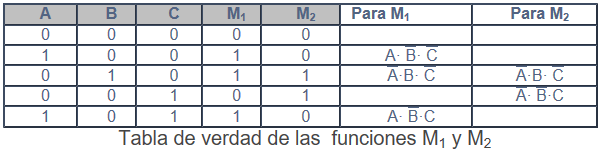
Para M1
M₁ = A·B·C + A·B·C + A·B·C = A·B(C+C) + A·B·C

de donde
M₁ = A·B + A·B· C
M₂ = A·B·C + A·B·C

Para M2

M₂ = A·B·C + A·B·C = A (B·C + B·C)

Mediante estas dos funciones resultantes nos permitirá trazar el circuito eléctrico y su esquema lógico, correspondiente, compruébese que cumple efectivamente las condiciones del enunciado.

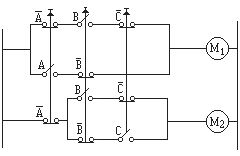
Fig. 4-9 – Circuito eléctrico que expresa
ambas funciones

Y ahora el esquema lógico:

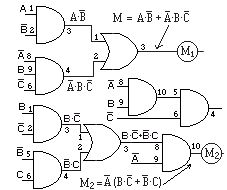
Fig. 4-10 -Esquema lógico de las dos funciones.

Observemos que la puerta Y, de tres entradas, se ha logrado con la combinación de dos puertas Y del mismo circuito integrado (CD4071B), véase la numeración de las patillas 8, 9 y 6 como entradas, la salida 10 y la entrada 5, logrando así, que nos de A·B· C en la salida 4. Dando un paso más estudiaremos un problema que contiene una célula de memoria.

CUARTO PROBLEMA.

Nos proponen controlar un motor eléctrico, mediante un interruptor general T con el que se da paso a la tensión del sistema, además mediante un pulsador P, se puede activar el motor siempre que la posición del eje del motor deje en reposo un contacto R.

El motor se pondrá en marcha si está cerrado T, si se pulsa P y siempre que a su vez el retén R se encuentre cerrado. En cambio si se abre el contacto del pulsador P no bastará para parar el motor ya que el mencionado contacto (retén o relé) R, puede que aún esté cerrado hasta llegar el eje a la posición de reposo (abierto), la figura nos aclarará lo expuesto.

Fig. 4-11 – Detector de posición

Fase 2, la tabla de verdad, sería:

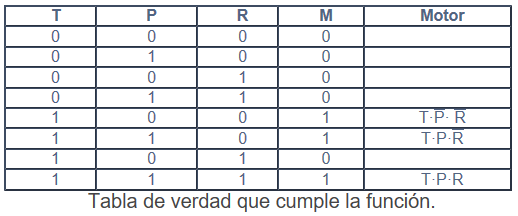
La fase 3, nos aporta la función:   M = T· P· R +T·P·R + T·P·R

Ahora tenemos que simplificar la ecuación.

a) -Sacamos T factor común;  M= T (P· R + P·R+P· R)
b) -Ahora sacamos factor común P, dentro del paréntesis: M = T [P·R + P(R + R) ]
c) -Dado que  R+ R = 1, queda que M = T (P · R + P)
d) -Dentro del paréntesis (P · R + P), se puede eliminar P, ya que no influye en el resultado,
compruébese en la figura 4-12.

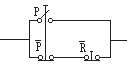
Fig. 4-12 -El término P no influye

 e) -Así, la función final queda simplificada y será: M = T (R · P)

Fase 4, el esquema eléctrico que será:

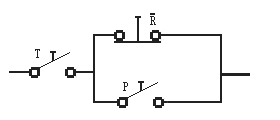
Fig. 4-13 – Esquema eléctrico.

Y fase 5, el diagrama lógico:

Fig. 4-14 – Diagrama lógico.

Creo que se puede dar por aclarado el tema.