Puentes de medida.
Puente de medida para tensión y corriente.
MEDIR CON UN mA.
En muchas ocasiones nos encontramos ante la necesidad de utilizar un miliamperímetro para realizar una medida o para adaptarlo a un proyecto que estamos realizando y nos resultaría adecuado pero nos plantea una duda, cómo conectarlo y que nos muestre con la mayor exactitud la magnitud de la medida que intentamos realizar.
Cuando tenemos que instalar un dispositivo de medida analógico o digital a un equipo como puede ser una fuente de alimentación, nos asaltan las dudas de cómo construir un puente divisor de tensión para crear una serie de escalas que podamos aprovechar y de este modo sacar el mayor rendimiento a nuestro trabajo. Cuando queramos utilizar un mA para montarlo como elemento de control visual en uno de nuestros proyectos, es conveniente recordar las reglas básicas para realizar una medida y no pasar por alto los importantes parámetros de los que dependerá la exactitud de nuestra medición. El miliamperímetro o galvanómetro será de imán permanente y bobina móvil.
Partimos de una posición comprometida, en algunas ocasiones nos interesaría realizar medidas de tensión y consumo de corriente con el mismo mA. en otras las posibilidades económicas nos permitirán disponer de dos dispositivos de medida para unas mejores prestaciones. En cualquier caso tenemos que apoyarnos en una cadena de divisores de tensión, dicho divisor, nos proporcionará los distintos rangos y por consiguiente de ellos obtendremos las sucesivas medidas de tensión o intensidad para el miliamperímetro o los miliamperímetros, según sea el caso.
Para realizar un puente divisor de tensión con cierta precisión nos debemos centrar en dos puntos esenciales de los cuales dependerá el éxito y la exactitud del puente de medida. Estos puntos en definitiva son, el dispositivo medidor que debe ser lo más exacto posible y el tipo de resistencias de precisión a utilizar. Trataremos de conseguir un galvanómetro de10 o 100 µA, o en su defecto un miliamperímetro de 1mA, es muy conveniente obtener las características del fabricante de este dispositivo a ser posible como la resistencia interna.
Los amperímetros se conectan en serie al circuito (con una baja resistencia o un shunt). Los voltímetros se conectan en paralelo y suelen tener una elevada resistencia interna que supera los 10kW. Supongamos que hemos conseguido un dispositivo de 1mA y no sabemos sus características, como su resistencia interna, aun así vamos a describir cómo se debe construir un medidor que satisfaga nuestras exigencias.
Antes de empezar deberíamos tener claro las subdivisiones para poder escalar los valores en que necesitamos movernos, para eso nos viene bien una tabla que nos facilite esta labor de conversión.
En cuanto a las resistencias que debemos utilizar es conveniente utilizar resistencias de película metálica del 1% o de película de carbón (carbón – film) del 1%, en cualquier caso de precisión. No es conveniente que sean de carbón estándar ya que suelen ser bobinadas y esto puede falsear la medida tomada. En la imagen que sigue, no se pueden apreciar las diferencias entre los tipos de resistencias.
Es dispositivo medidor si no puede ser de 100 µA debemos conseguir uno de 1mA, el precio puede ser el mayor inconveniente a la hora de decidirse.
CASO DEL VOLTÍMETRO.
Ahora, deberemos tomar la decisión más comprometida, se trata de saber cuantas escalas deseamos, una vez decidido este punto, ya sólo nos queda calcular los valores de las resistencias que necesitaremos adquirir para construir el puente de medida. En general el cálculo de las resistencias a colocar en serie en los voltímetros (galvanómetro), se hace con esta fórmula:
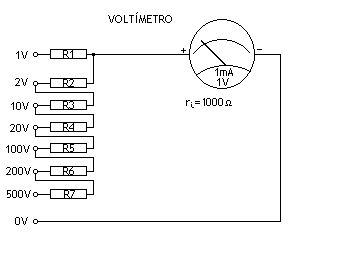
No obstante, en la figura 3, la disposición de las distintas resistencias se acumulan en serie y hemos de proceder con una pequeña variación a la fórmula [1]. Como se trata de un ejercicio en práctica, vamos a disponer de 7 entradas o dicho de otro modo, de 7 escalas de medida y el común.
Hemos sometido el anterior esquema para construir nuestro voltímetro. Ahora, calcularemos los valores de cada resistencia de modo que las escalas de tensión se correspondan.
Para:
R1 = 0W (el miliamperímetro directo = 1V)
R2 = 2-1/0’001 = 1kW
R3 = 10-2/0’001 = 8kW
R4 = 20-10/0’001 = 10kW
R5 =100-20/0’001 = 80kW
R6 =200-100/0’001 = 100kW
R7 =500-200/0’001 = 300kW
Como podemos ver, todos los valores obtenidos son bastante sencillos de lograr ya que, en alta calidad (1%) los saltos de valores en las resistencias son más cercanos, de todos modos es fácil implementar el valor con series de valores, para lograr el deseado.
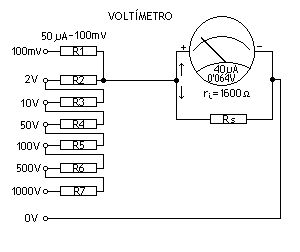
Veamos otro ejemplo para un caso distinto, sea un microamperímetro de 40µA como el de la figura 4.
Calculemos los valores de estas resistencias para que cumplan los parámetros expresados en la misma figura. Tengamos en cuenta la resistencia Rs en ‘shunt’ con el microamperímetro.
Para:
VR1 <> 50µA – 100mA
Rs = 0’064/1*10-5 = 6.400W
R1 = 0’1-0’064/50*10-5 = 720W
R2 = 2-0’064/50*10-5 = 38.720W
R3 = 10-2/50*10-5 = 160kW
R4 = 50-10/50*10-5 = 800kW
R5 = 200-50/50*10-5 = 3MW
R6 = 500-200/50*10-5 = 6MW
R7 =1000-500/50*10-5 = 10MW
Consideramos que con estos dos ejemplos pueden servirnos como base para cualquier aplicación similar. Ahora, sigamos.
CASO DEL AMPERÍMETRO.
Cuando necesitamos conocer la corriente de paso o dicho de otra forma el consumo de una carga o receptor, necesitamos disponer de un miliamperímetro intercalado en dicho circuito. En esta práctica vamos a considerar la construcción de un amperímetro con varias escalas que nos faciliten la labor en la medición de la intensidad que circula por el circuito de un equipo o una instalación industrial.
Debido a que la intensidad de la corriente suele ser un factor bastante desconocido a priori y se necesita disponer el miliamperímetro en serie con el circuito, es muy arriesgado elegir la escala de intensidad a conmutar, para evitar la destrucción la bobina del galvanómetro del medidor. Por lo tanto, es preceptivo al tomar una medida una vez más, optar por la escala de mayor rango. Antes, en la figura 4, de pasada hemos empleado una resistencia en ‘shunt’ con el mili-amperímetro. En el caso de un amperímetro, como estamos abordando, es interesante tener claro el uso y cálculo de las resistencias en ‘shunt’, por lo que sería interesante leer el tema leyes básicas, en el que se describe con amplitud.
Así, en ocasiones como ya se ha dicho, es conveniente utilizar un miliamperímetro o voltímetro para medir magnitudes eléctricas que requieren de una escala más alta que la que nos ofrece el instrumento que se dispone. Para estos casos, es necesario añadirle unas resistencias. Al cociente del valor máximo de la nueva escala dividido por el valor máximo de la escala primaria, es lo que se llama factor de multiplicación como se obtiene en la formula [2].
La cual podemos recordar mejor con esta nueva formula [2a].
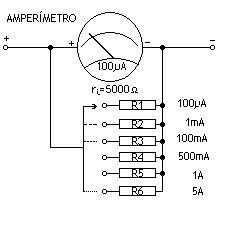
En la figura 5, se presenta el esquema de nuestra práctica. En ella vemos un microamperímetro de 100µA y una resistencia interna de 5kW con el que queremos construir un dispositivo que nos permita medir los rangos que se aprecian en la citada figura.
Calculemos los valores de estas resistencias para que cumplan los parámetros expresados. Primero hallaremos las intensidades que les corresponden a cada entrada.
Para:
V0 = 0’0001 * 5000 = 0’5 = 500mV ; para la entrada directa.
IR1 = 0’001-0’0001 = 0’0009A
IR2 = 0’1 – 0’0001 = 0’0999A
IR3 = 0’5 – 0’0001 = 0’4999A
IR4 = 1 – 0’0001 = 0’9999A
IR5 = 5 – 0’0001 = 4’9999A
Ahora calcularemos los valores que corresponden a las resistencias.
Para:
R1 = 0’5/0’0009 = 555’555Ω
R2 = 0’5/0’0999 = 5’005Ω
R3 = 0’5/0’4999 = 1’000Ω
R4 = 0’5/0’9999 = 0’500Ω
R5 = 0’5/4’9999 = 0’100Ω
Y con esto, queda resuelto el problema propuesto.
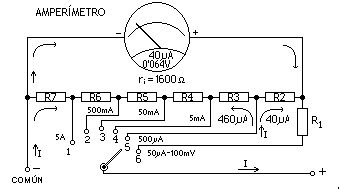
Veamos otro ejemplo con una evidente diferencia en la construcción. En esta ocasión según se aprecia en la figura siguiente todas las resistencias se encuentran de algún modo sometidas al paso de la corriente, la cual dispone de dos caminos para su recorrido, pero como siempre una imagen mejor que …
Sabemos que la resistencia total RT (R7+R6+R5+R4+R3+R2=6400W ), en la figura destacan los dos caminos que sigue la corriente en el rango de 500µA, un camino, la entrada [500µA] de 460µA y el y el otro camino de 40µA por la resistencia R2.
RT = R7 + R6 + R5 + R4 + R3 + R2 = 6.400W
R1 = 0’1-0’064/5•10-5 = 720W ; ahora
La solución pasa por resolver la ecuación de tres incógnitas E1, E2 y E3. Sustituyendo
Que sustituyendo de nuevo
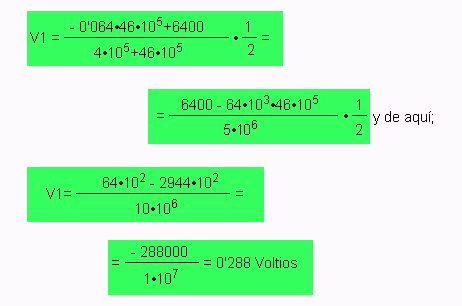
Saquemos V1 factor común.
Así, tenemos que la tensión a extremos de R2 es de 0’288V, que sumados a los 0’046V del miliamperímetro tenemos 0’334V. Ya que las tensiones presentes a extremos de resistencias en paralelo son idénticas, estos 0’334V son los mismos que habrá a extremos del conjunto R3-7, que es la otra rama del paralelo, por lo tanto podemos hallar el valor de R2 y del conjunto R3-7. Veamos:
Del mismo modo podemos encontrar el valor de cada una de las resistencias restantes.
Se ha añadido la tabla de conversión.
Consideramos que este documento ha tratado y clarificado bastante el tema, con lo que puede darse por concluido, creo que puede servir a muchos aficionados a la electrónica a resolver los casos que se le puedan presentar en este campo.
Los comentarios serán bien recibidos.
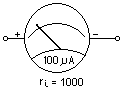


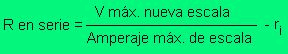
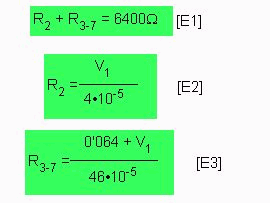





0 comentarios